Introducción a NetworkX
- 116 minsIntroducción a NetworkX¶
Rodolfo Ferro (ferro@cimat.mx)
¿Qué es NetworkX?¶
- NetworkX es una biblioteca de Python diseñada para la creación, manipulación y análisis de estructuras de grafos y redes complejas.
- Es utilizada en diversas disciplinas, como ciencia de datos, optimización de redes, bioinformática, redes sociales y más.
- Permite trabajar con grafos dirigidos, no dirigidos y con pesos.
¿Qué es un Grafo?¶
- Un grafo es una estructura compuesta por nodos (también llamados vértices) y aristas (edges o arcos) que conectan estos nodos. Es decir, $G = {V, E}$.
- Los grafos pueden ser:
- Dirigidos: las aristas tienen dirección (e.g., Twitter).
- No dirigidos: las aristas no tienen dirección (e.g., Facebook).
- Con pesos: las aristas tienen un valor asociado (e.g., distancias, costos).
- Cíclicos o acíclicos: Si llegan a tener (o no) un camino cerrado entre sus nodos, es dcir, que vuelve a un nodo inicial.
- Los grafos son representaciones matemáticas de relaciones entre entidades.
Representación de un Grafo¶
Si bien, los grafos pueden ser representados gráficamente ilustrando los nodos y sus conexiones, los grafos pueden ser representados computacionalmente de diferentes formas, por ejemplo:
- Matriz de incidencia: una matriz cuadrada donde cada celda $(i,j)$ indica si existe una arista entre los nodos $i$ y $j$.
- Matriz de adyacencia: una matriz cuadrada donde cada celda $(i,j)$ indica el peso de conexión de la arista entre los nodos $i$ y $j$.
- Lista de adyacencia: cada nodo tiene una lista de sus nodos vecinos.
- Diccionarios: donde las claves son los nodos y los valores son listas de nodos conectados.
En NetworkX, se utiliza la representación de diccionario de adyacencia, pero también se pueden convertir a matrices de adyacencia u otras representaciones.
EJEMPLO:¶
Consideremos el siguiente grafo:
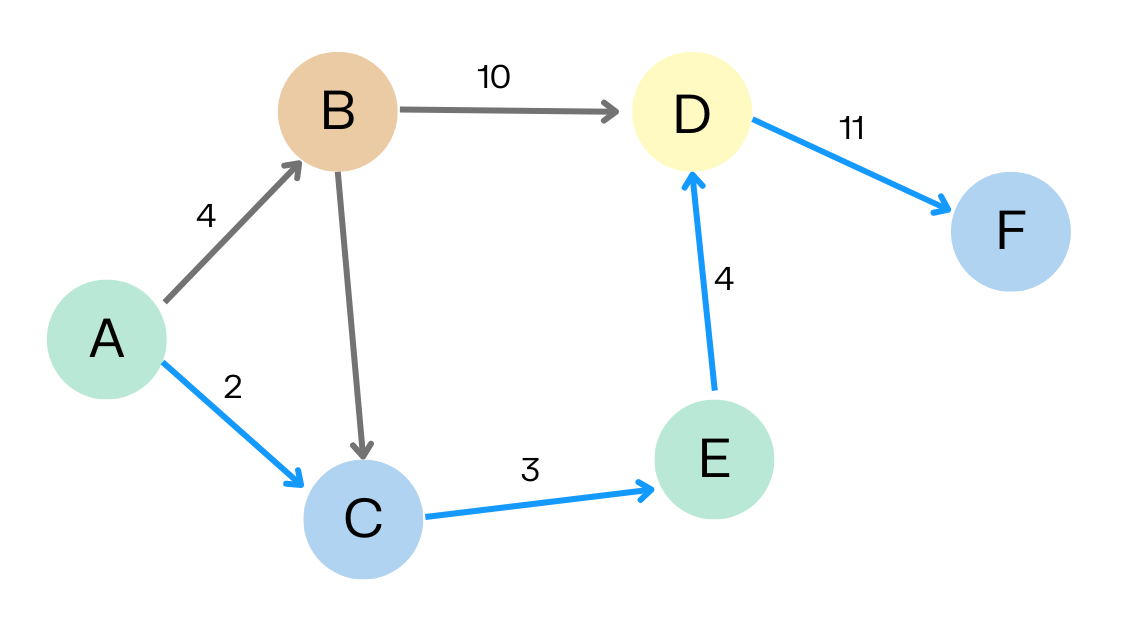
Primero, notemos que este es un grafo:
- Dirigido: porque sus aristas tienen dirección.
- Acíclico: porque no existe nodo alguno que al seguir un camino, llegue al mismo.
- Pesado: porque las aristas tienen un valor de costo/peso asociado.
Su representación con una matriz de incidencia sería:
$$ \hspace{1.5cm} \begin{matrix} A \hspace{0.5cm} B \hspace{0.5cm} C \hspace{0.5cm} D \hspace{0.5cm} E \hspace{0.5cm} F \end{matrix}\\ \hspace{0.9cm} \begin{matrix} ↓ \hspace{0.5cm} ↓ \hspace{0.5cm} ↓ \hspace{0.5cm} ↓ \hspace{0.5cm} ↓ \hspace{0.5cm} ↓ \end{matrix}\\ \begin{matrix} A → \\ B → \\ C → \\ D → \\ E → \\ F → \end{matrix} \begin{pmatrix} 0 & 1 & 1 & 0 & 0 & 0\\ 0 & 0 & 1 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 \end{pmatrix} $$
Notemos que si fuese un grafo no dirigido, su matriz de incidencia sería simétrica.
Su representación con una matriz de adyacencia sería:
$$ \hspace{1.5cm} \begin{matrix} A \hspace{0.5cm} B \hspace{0.5cm} C \hspace{0.5cm} D \hspace{0.5cm} E \hspace{0.5cm} F \end{matrix}\\ \hspace{0.9cm} \begin{matrix} ↓ \hspace{0.5cm} ↓ \hspace{0.5cm} ↓ \hspace{0.5cm} ↓ \hspace{0.5cm} ↓ \hspace{0.5cm} ↓ \end{matrix}\\ \begin{matrix} A → \\ B → \\ C → \\ D → \\ E → \\ F → \end{matrix} \begin{pmatrix} 0 & 4 & 2 & 0 & 0 & 0\\ 0 & 0 & 1 & 10 & 0 & 0\\ 0 & 0 & 0 & 0 & 3 & 0\\ 0 & 0 & 0 & 0 & 0 & 11\\ 0 & 0 & 0 & 0 & 4 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 \end{pmatrix} $$
Notemos nuevamente que si fuese un grafo no dirigido, su matriz de adyacencia también sería simétrica.
Creación de Grafos¶
Definición: Un grafo es una estructura compuesta por nodos (vértices) y conexiones entre ellos (aristas, edges o arcos). NetworkX facilita su creación mediante estructuras de datos flexibles.
# Importar bibliotecas necesarias.
import networkx as nx
import numpy as np
import matplotlib.pyplot as plt
Ejemplo: Creación de un grafo simple
Explicación:
- Se crea un grafo vacío.
- Se añaden nodos individualmente o en conjunto.
- Se agregan aristas entre los nodos.
# Sección 1: Creación de un Grafo Simple
# Crear un grafo no dirigido y añadir nodos y aristas
G = nx.Graph()
G.add_nodes_from(["A", "B", "C", "D"])
G.add_edges_from([
("A", "B"), # Arista A <-> B
("B", "C"), # Arista B <-> C
("C", "D") # Arista C <-> D
])
# Mostrar detalles del grafo
print("Nodos:", G.nodes)
print("Aristas:", G.edges)
# Visualización del grafo
nx.draw(
G,
with_labels=True,
node_color='lightblue',
edge_color='gray'
)
plt.show()
Nodos: ['A', 'B', 'C', 'D']
Aristas: [('A', 'B'), ('B', 'C'), ('C', 'D')]
Notemos lo siguiente:
- Podemos crear un grafo vacío con
nx.Graph(). - Podemos agregar nodos y aristas al grafo vacío.
- Podemos explorar los nodos del grafo con
G.nodesyG.edges, respectivamente. - Este gráfo es no dirigido (para grafos dirigidos se usa
nx.DiGraph). - El despliegue del grafo es aleatorio (no se han seteado coordenadas/posiciones para los nodos). Esto se puede explorar en la sección avanzada.
Crear un grafo desde una matriz de incidencia¶
Definición: Una matriz de incidencia es una representación de un grafo en una matriz cuadrada, donde cada fila y columna representan un nodo y las entradas indican si existe una arista entre los nodos correspondientes.
# Sección 2: Crear un grafo desde una matriz de incidencia
# Crear una matriz de incidencia
inc_matrix = np.array([[0, 1, 1, 0],
[1, 0, 1, 0],
[1, 1, 0, 1],
[0, 0, 1, 0]])
# Crear un grafo desde la matriz de incidencia
G_from_matrix = nx.from_numpy_array(inc_matrix)
# Mostrar nodos y aristas
print("Nodos del grafo desde matriz:", G_from_matrix.nodes)
print("Aristas del grafo desde matriz:", G_from_matrix.edges)
# Visualización del grafo creado desde la matriz de incidencia
nx.draw(G_from_matrix, with_labels=True, node_color='lightblue', edge_color='gray')
plt.show()
Nodos del grafo desde matriz: [0, 1, 2, 3] Aristas del grafo desde matriz: [(0, 1), (0, 2), (1, 2), (2, 3)]
Notemos lo siguiente:
- Podemos crear un grafo y definir sus conexiones desde un array de Numpy con
nx.from_numpy_array(). - Notemos que es no dirigido, por lo que la matriz de incidencia es simétrica.
- La matriz de incidencia simplemente indica si hay conexiones en $(i, j)$, o es el caso particular de adyacencia con peso 1.
Crear un grafo con pesos desde una matriz de incidencia¶
Definición: Cuando se asignan pesos a las aristas de un grafo, la matriz de adyacencia puede contener valores distintos de 1 para indicar el peso de cada arista.
Ejemplo: Crear un grafo ponderado.
Explicación:
- En la matriz de adyacencia, los valores distintos de 0 representan el peso de las aristas entre los nodos correspondientes.
- Se crea un grafo ponderado.
- Las aristas devuelven los pesos asociados.
# Sección 3: Crear un grafo ponderado desde una matriz de adyacencia
# Crear una matriz de adyacencia
adj_matrix_weighted = np.array([[0, 2, 0, 0],
[2, 0, 3, 0],
[0, 3, 0, 4],
[0, 0, 4, 0]])
# Crear un grafo ponderado
G_weighted = nx.from_numpy_array(adj_matrix_weighted)
# Mostrar aristas con sus pesos
print("Aristas con peso:", G_weighted.edges(data=True))
# Visualización del grafo ponderado
pos = nx.spring_layout(G_weighted, seed=123)
nx.draw(
G_weighted,
pos,
with_labels=True,
node_color='lightblue',
edge_color='gray'
)
# Agregamos etiquetas a las aristas
labels = nx.get_edge_attributes(G_weighted, "weight")
nx.draw_networkx_edge_labels(G_weighted, pos, edge_labels=labels);
plt.show()
Aristas con peso: [(0, 1, {'weight': 2}), (1, 2, {'weight': 3}), (2, 3, {'weight': 4})]
Notemos lo siguiente:
- Podemos crear un grafo ponderado y definir sus conexiones desde un array de Numpy con
nx.from_numpy_array(). - Notemos que es no dirigido, por lo que la matriz de adyacencia es simétrica.
- La matriz de adyacencia indica el peso de las conexiones en $(i, j)$.
- Definimos posiciones a través de un layout fijo, usando
nx.spring_layout(). - Obtuvimos los valores de los pesos para usarlos como etiquetas con
nx.get_edge_attributes(). - Le pasamos el parámetro
posa los métodos para desplegar los grafos.
Crear un grafo dirigido desde una matriz de incidencia¶
Definición: Un grafo dirigido es aquel en el que las aristas tienen una dirección, lo que significa que las relaciones entre los nodos son unidireccionales.
Ejemplo: Crear un grafo dirigido.
Explicación:
- La matriz de adyacencia representa un grafo dirigido con relaciones unidireccionales.
- Se utiliza el parámetro
create_using=nx.DiGraphpara especificar que el grafo debe ser dirigido. - Se pueden acceder a las aristas del grafo dirigido.
# Sección 4: Crear un grafo dirigido desde una matriz de incidencia
# Crear una matriz de incidencia para un grafo dirigido
adj_matrix_directed = np.array([[0, 1, 0, 0],
[0, 0, 1, 0],
[0, 0, 0, 1],
[0, 0, 0, 0]])
# Crear un grafo dirigido
G_directed = nx.from_numpy_array(adj_matrix_directed, create_using=nx.DiGraph)
# Mostrar aristas dirigidas
print("Aristas dirigidas:", G_directed.edges)
# Visualización del grafo dirigido
nx.draw(
G_directed,
with_labels=True,
node_color='lightblue',
edge_color='gray',
arrows=True
)
plt.show()
Aristas dirigidas: [(0, 1), (1, 2), (2, 3)]
Propiedades de los Grafos¶
- Grado de un nodo: El número de aristas conectadas a un nodo.
- Conectividad: Determina si existe un camino entre todos los nodos.
- Ciclo: Un camino cerrado en el que el primer y último nodo coinciden.
- Componentes conexas: Subgrafos donde cada par de nodos está conectado entre sí.
# Sección 5: Propiedades de los Grafos
# Grado de un nodo
degree = G.degree("A")
print("Grado del nodo 'A':", degree)
# Conectividad (comprobamos si el grafo es conexo)
is_connected = nx.is_connected(G)
print("¿El grafo es conexo?", is_connected)
# Componentes conexas
components = list(nx.connected_components(G))
print("Componentes conexas:", components)
Grado del nodo 'A': 1
¿El grafo es conexo? True
Componentes conexas: [{'B', 'A', 'D', 'C'}]
Visualización de Grafos¶
NetworkX permite la visualización de grafos utilizando Matplotlib.
Como hemos visto hasta ahora:
- Se puede desplegar el grafo con etiquetas.
- Se pueden personalizar colores de nodos y aristas.
- Se muestra el grafo en pantalla.
Métodos y Parámetros - Dijkstra¶
Definición: El algoritmo de Dijkstra encuentra el camino más corto desde un nodo origen a un nodo destino en un grafo ponderado.
¿Cómo funciona el algoritmo de Dijkstra?¶
- El algoritmo comienza desde el nodo de origen y explora todos los caminos hacia los nodos vecinos, siempre eligiendo el nodo más cercano.
- Para cada nodo, se calcula la distancia más corta desde el nodo origen.
- A medida que se exploran los nodos, se actualiza la distancia más corta conocida.
- Al final, se obtiene el camino más corto entre el nodo origen y el nodo destino.
Ejemplo de implementación.
Explicación de parámetros:
source="A": Nodo de origen.target="D": Nodo de destino.weight=None(Opcional): Especifica que el grafo no tiene pesos. Si tuviera pesos, se indicaría el nombre del atributo del peso.
# Sección 6: Algoritmo de Dijkstra
# Grafo ponderado para Dijkstra
G_weighted.add_edge("A", "D", weight=5)
G_weighted.add_edge("B", "D", weight=3)
# Encontrar el camino más corto usando el algoritmo de Dijkstra
shortest_path = nx.shortest_path(G_weighted, source="A", target="D", weight="weight")
print("Camino más corto de A a D:", shortest_path)
Camino más corto de A a D: ['A', 'D']
Flujo Máximo en Redes¶
Definición: El problema de flujo máximo busca encontrar la mayor cantidad de flujo que puede moverse de un nodo origen a un nodo destino en una red con capacidades limitadas.
Ejemplo.
# Sección 7: Flujo Máximo
# Crear un grafo de flujo con capacidades
G_flow = nx.DiGraph()
G_flow.add_edge("A", "B", capacity=4)
G_flow.add_edge("A", "C", capacity=5)
G_flow.add_edge("B", "C", capacity=3)
G_flow.add_edge("B", "D", capacity=2)
G_flow.add_edge("C", "D", capacity=3)
# Calcular el flujo máximo entre A y D
flow_value, flow_dict = nx.maximum_flow(G_flow, "A", "D")
print("Flujo máximo de A a D:", flow_value)
print("Distribución del flujo:", flow_dict)
Flujo máximo de A a D: 5
Distribución del flujo: {'A': {'B': 4, 'C': 1}, 'B': {'C': 2, 'D': 2}, 'C': {'D': 3}, 'D': {}}
Avanzado - Re-etiquetado y pocisionamiento¶
Avanzado: Renombrar nodos.¶
# Crear una matriz de adyacencia
adj_matrix = np.array([[0, 1, 1, 0],
[1, 0, 1, 0],
[1, 1, 0, 1],
[0, 0, 1, 0]])
# Crear un grafo desde la matriz de adyacencia
G_from_matrix = nx.from_numpy_array(adj_matrix)
pos_G = nx.spring_layout(G_from_matrix, seed=123)
# Aplicamos remapeo de etiquetas
mapping = {0: "A", 1: "B", 2: "C", 3: "D"}
H = nx.relabel_nodes(G_from_matrix, mapping)
pos_H = nx.spring_layout(H, seed=123)
Notemos:
- Usamos la función
nx.relabel_nodes()para renombrar etiquetas, la información se propaga en el grafo. Es necesario proveer el diccionario de remapeo de etiquetas. - Esto es útil cuando construimos a partir de un array de Numpy y queremos renombrar las etiquetas.
Desplegamos el grafo original con etiquetas:
# Graficamos G
nx.draw(
G_from_matrix,
pos_G,
with_labels=True,
node_color="tomato",
edge_color="gray"
)
Desplegamos el grafo con nuevas etiquetas:
# Graficamos H
nx.draw(
H,
pos_H,
with_labels=True,
node_color="tomato",
edge_color="gray"
)
Avanzado: Asignar posiciones a los nodos.¶
from pprint import pprint
# Se puede obtener una representaicón plana
pos = nx.planar_layout(H)
print("Diccionario de posiciones:")
pprint(pos)
# Desplegamos representación plana con posiciones dadas
nx.draw(H, pos)
Diccionario de posiciones:
{'A': array([-1. , -0.33333333]),
'B': array([ 0.77777778, -0.33333333]),
'C': array([0.33333333, 0.11111111]),
'D': array([-0.11111111, 0.55555556])}
Como hemos visto, al usar la función nx.planar_layout() o nx.spring_layout() se genera un diccionario de pocisiones fijas (aleatorias).
Lo importante de aquí es notar la estructura de las pocisiones, puesto que es el parámetro que nos interesa modificar.
En este caso, observamos que la estructura es un diccionario:
{'A': array([-1. , -0.33333333]),
'B': array([ 0.77777778, -0.33333333]),
'C': array([0.33333333, 0.11111111]),
'D': array([-0.11111111, 0.55555556])}
Por lo que podemos crear una estructura similar con las pocisiones deseadas.
Creamos un nuevo grafo y aplicamos todo:
- Redefinimos los nombres de las etiquetas en los nodos.
- Modificamos las pocisiones en los mismos.
# Con la estructura anterior se pueden especificar
# las posiciones (x, y) de los nodos en un grafo
# Crear una matriz de adyacencia
adj_matrix = np.array([
[0, 6, 4, 0, 0, 0],
[6, 0, 2, 2, 0, 0],
[4, 2, 0, 1, 2, 0],
[0, 2, 1, 0, 1, 7],
[0, 0, 2, 1, 0, 3],
[0, 0, 0, 7, 3, 0]
])
# Crear un grafo desde la matriz de adyacencia
G = nx.from_numpy_array(adj_matrix)
# Aplicamos remapeo de etiquetas
mapping = {item: item + 1 for item in range(7)}
G = nx.relabel_nodes(G, mapping)
# Desplegamos G antes del repocisionamiento
nx.draw(G, with_labels=True, node_color="tomato", edge_color="gray")
# Ajustamos posiciones
pos = {
1: np.array([-1.5, 0.5]),
2: np.array([ 0.0, 0.0]),
3: np.array([ 0.0, 1.0]),
4: np.array([ 3.0, 0.0]),
5: np.array([ 3.0, 1.0]),
6: np.array([ 4.5, 0.5]),
}
# Desplegamos G con posiciones
plt.figure(figsize=(3, 2), dpi=300)
nx.draw(G, pos, with_labels=True, node_color="lightgreen", edge_color="gray")
# Agregamos etiquetas a las aristas
labels = nx.get_edge_attributes(G, "weight")
nx.draw_networkx_edge_labels(G, pos, edge_labels=labels);
